Football-Data's revenues come from losses accrued by customers of advertised bookmakers. Nearly all bettors lose in the long run. Users taking advantage of any advertised welcome offer should familiarise themselves with the bookmaker's T&Cs. Any information appearing on this website, including references to winning, profit, beating odds/bookmakers etc. should not be considered professional advice or a recommendation to bet or gamble. Furthermore, the small proportion of customers considered by bookmakers to be sufficiently skilled at beating their prices may find their stakes restricted or have their accounts closed. Both the UK Government and bookmakers alike maintain that betting and gambling in the UK should be considered a form of entertainment only and not a trade to make money. Please gamble responsibly. NEVER risk what you cannot affort to lose. GambleAware.

Wisdom of the Crowd Applied to Tennis Match Betting

In August 2015 (updated June 2017), I published an article describing a possible football betting system based on the Wisdom of the Crowd. The methodology assumes that the Pinnacle football match betting market (1X2) offers the most efficient (accurate) prices, which once adjusted for the margin and the favourite-longshot bias, should provide reasonable estimates for fair odds. Consequently, where other bookmakers are found to be offering longer prices, the presumption is that these represent betting value. The nature of the system allows the user to calculate expected value for every bet and hence the expected average advantage held over the profit line. I've have now applied the Wisdom of the Crowd methodology to tennis match betting and the purpose of this article is to review the results.

My network website tennis-data.co.uk has historical results and match betting odds data for the ATP and WTA circuits dating back to 2000. Since 2010 the data files have contained both closing odds from Pinnacle and accompanying best market odds selected from a variety of online sports bookmakers. After removing matches with missing odds, obvious errors, walkovers and retirements where a single set had not yet been completed, I was left with a sample 66,035 player betting odds.

As with for the football 1X2 version of this methodology, the first step is to remove Pinnacle's betting margin from the odds, with a view to estimating the fair or 'true' probability of every result. The significant difference here is that we are dealing with a two-way market, rather than three. The updated Wisdom of the Crowd PDF describes three methodologies for undertaking this which take into account the now familiar favourite-longshot bias: Margin Weights Proportional to the Odds, Odds Ratio and Logarithmic Function. My available 'true odds' betting calculator makes these methodologies available again for two-way markets. For two-way markets I have found that the logarithmic function tends to overestimate the strength of the favourite-longshot bias, such that when removing the margin, longer odds are a little longer than they should be. Returns from blind betting these 'true odds' to level stakes were 101.15%. By contrast, the odds-ratio methodology appeared to offer a better fit for determining 'true odds', with equivalent returns 100.19%, much closed to the expectation of 100%.

With 'true odds' calculated, the assumption again is that the ratio of bookmaker odds to the 'true odds' provides a useful measure of value expectation. For example, if the calculated 'true odds' is 2.00 and another bookmaker has a price of 2.10, then the expected value for this bet is 2.10/2.00 = 1.05 or +5%. In contrast, if the bookmaker's odds were 1.90, the expected value would be 1.90/2.00 = 0.95 or -5%. For simplicity for the remainder of this article I will call this ratio the WOC ratio.

Blanket betting all 66,035 best market prices to level stakes returned 99.1% (expected 99.0%). Of these, there were 25,350 selections where the WOC ratio was greater than 1.00 (implying profitable expectation). The return from these selections was 101.7% (expected 102.5%). The profit chart over those theoretical wagers is shown in the first chart below. Despite a midterm dip in performance, there is evidently a reasonable profit trend broadly mirroring expectation, although the final return falls a little short.

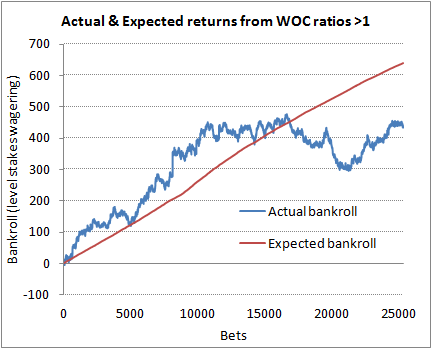
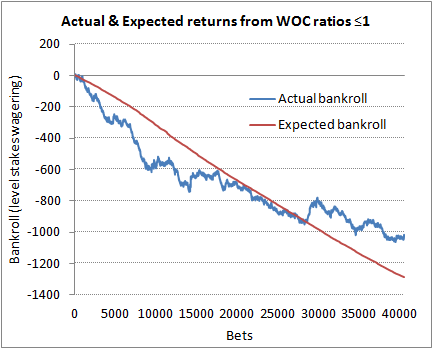
In contrast, there were 40,685 selections where the WOC ratio was equal to or less than 1.00, and these returned 97.5% (expected 96.8%). A similar profit chart for these theoretical wagers is also shown. Again, actual performance broadly matches expectation.

The table below compares actual performance and expectation for a range of WOC ratio thresholds.

These figures are then shown in the scatter plot below.

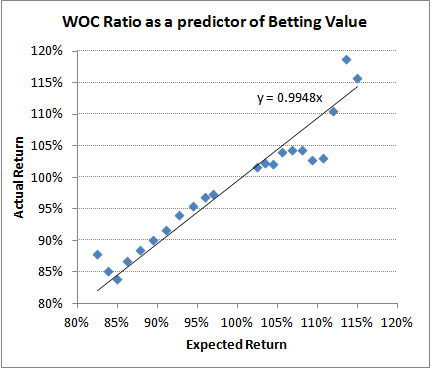
Whilst it's probably inappropriate to plot a trend line illustrating the general relationship between expected and actual returns on account of the vastly different sample sizes for varying threshold ratios, the outcome is nonetheless very satisfying, revealing an almost perfect one to one relationship between predictor (expected return) and predicted (actual return) variables. Certainly it is true that actual returns failed to keep pace with expected returns as the WOC ratio threshold increased above 1.00, although we are probably justified in arguing that much of this is down to statistical variance on account of decreasing sample sizes more than a failure of the model.

Of course as with any betting system of this nature there are two important caveats. Firstly, we cannot guarantee that it will continue to behave as in this retrospective analysis. Should other bookmakers seek to improve the efficiency of their odds relative to Pinnacle's in the future, this will weaken the model validity. Secondly, as with any potentially profitable betting system that uncovers real profitable expectation, get those bets accepted at bookmakers who don't like advantage punters will potentially prove to be an even bigger task than finding profitable expectation in the first place.