Is Sports Betting Completely Random?
Posted 25th March 2015
Over the years I've had many debates with punters and tipsters about the possibilities of making a consistent profit through skill, or whether in fact sports betting is nothing more than a random game of chance. The overwhelming majority, who are in favour of the argument that long term profits are possible, generally fall back on the argument that sports betting is not coin tossing or roulette, where the probabilities of all possible outcomes are perfectly known according to mathematical first principles. On the contrary, precisely because the probabilities of sporting outcomes can never be known a priori, this creates opportunities to take advantage of mistakes others make when trying to estimate these probabilities. Economists call this market inefficiency. Undoubtedly, mistakes will always be made in estimating the probabilities of sporting outcomes. The key point, however, is whether these mistakes or inefficiencies are in anyway sufficiently systematic to allow their prediction and to enable a sports bettor to consistently make a profit. I've highlighted these words for a reason.
For profits to be consistent and predictable they must be based on more than chance. The law of large number ensures that good and bad luck will inevitably cancel each other out the longer we play in a game that involves uncertainty. In sports betting, if there is nothing other than chance operating, the expectation will be that in the long run the bettor will lose an amount of money predicted by the size of the commission he is paying to the bookmaker(s). But how can we test for whether there is something more than chance?
In 2013 I wrote an article reviewing the statistical technique of testing for evidence of betting skill. This method utilises the student's t-test to look for statistically significant differences between a bettor's record and what would be expected to occur by chance. Specifically, the test produces a probability that a betting record could have arisen in the event that nothing more than chance was operating. What it does not do is inform the user of the chances that the betting record had arisen by skill. So the following problem then arises: what if we have 100 records and 1 of them has a 1 in 100 probability of arising by chance; what if we have 1,000 records and 1 of them has a 1 in 1,000 probability of arising by chance. Essentially we are still no nearer knowing absolutely whether what happened did so because of something more. Unfortunately this is the general shortcoming of all statistics. Being as it is a method of induction it can never provide the user with absolute certainty. All answers are inherently probabilistic.
What we can do is compare many betting record samples to what we might have expected to have seen if only chance was operating; the bigger the sample the more reliable the conclusions. In my previous article analysing the tipping service Botprediction.com I revealed how we might attempt to show graphically the difference between lucky profits and ones that had happened because of something the forecaster had done. Random stochastic processes, like coin tossing, where there is no memory between events and nothing predictable via past behaviour, show binomial (or normal) distributions, bell-shaped curves that most school students will have a vague memory of. Most outcomes cluster around the expected average, with fewer at the extremes.
Botprediction, however, was implicitly just tossing coins via the mechanism of what it was doing (creating predictive robots by means of a random number generator), even if the owner was unintentionally (or perhaps deliberately) misleading users to the contrary. What about real human beings, with rationalities and emotions, capable of accessing variable sources of information and constructing numerous hypotheses about causal relationships between predictive variables and the outcome of sporting contests? Surely they can't be tossing coins too, can they? For this article I have repeated this comparative analysis between observation and chance for a 1-million tip sample provided by the tipping social network Pyckio.com, of which I should declare I am a 5% shareholder.
Pyckio launched on the 12th June 2014. By the 10th February 2015 it had received 1,073,029 picks (excluding unsettled bets) from 6,044 different tipsters, with an average odds of 1.99. All tips must be advised with the sportsbook Pinnacle Sports, known for suitable liquidity for most markets and an acceptance of winning punters. Markets on which one can tip have been restricted to the following: American football, Australian football, baseball, basketball, darts, e-sports, handball, hockey, mixed martial arts, rugby, snooker, soccer, table tennis, tennis and volleyball. Tipsters are permitted to stake in the range 1 to 10 units, but Pyckio also analyses performance for every tipster to level stakes. Almost all tipsters are currently free to follow, with just a tiny number of the best performers rated as PRO, which require a subscription fee. This contrasts with nearly all other subscription based tipster platforms which charge a fee for every tipster.
Below is the time series profit chart for all 1,073,029 picks analysed to level stakes. Whilst one might argue that I should do so using the actual stakes, the reader should understand that different money management in no way changes the long term expectations but merely the nature of risks over shorter time scales. Level stakes analysis is the most useful method to determine whether a tipster, or collection of tipsters, has an advantage over that expected by chance alone. Furthermore, a handful of tipsters have been attempting to manipulate their ratings by using artificial staking methods that would be of little practical benefit to customers in the real world. Level stakes allows us to see behind this manipulation.
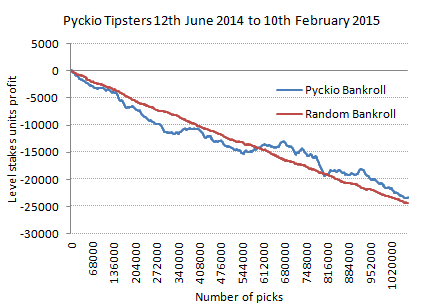
The aggregated yield for the full record was -2.17%. Readers will immediately notice that this is pretty close to the typical profit margin employed by Pinnacle Sports for most of its markets. [Note that a punter's loss expectancy is given by the equation 1/bookmaker's margin -1, where the margin is express as a decimal.] Also shown in the time series is a bankroll trend that we might expect to witness simply by chance. To model a series of random betting outcomes, I first assumed an average profit margin in the Pinnacle betting prices of 2.5% (1.025 in decimal notation). Whilst markets for minor sports have margins higher than this, the majority of tips advised through Pyckio have been for soccer, tennis and US sports, all with margins in the region of about 2.1 to 2.2%. I then included the influence of the favourite-longshot bias. This pricing bias arises because punters tend to overbet longshots whilst under betting favourites. Consequently, long prices are probably shorter than they should be, whilst short prices are somewhat more generous, compared to fully rational expectations. In applying differential margins to shorter and longer prices respectively, I have assumed that the margin weights are proportional to the outcome probabilities defined by the odds. For example, a price of 1.50 would have a margin of 1.25% (1.0125) whilst a price of 3.00 would have a margin of 5% (1.05). Whilst this method is simply an estimation, I have observed that the prices it provides follow remarkably well those offered by Pinnacle Sports. With expectancies for every tip calculated, it was then a simple matter of using a random number generator to determine whether a tip won or lost.
The yield from random outcomes was -2.27%, almost exactly the same as for the actual yield. There was no statistically significant difference between the two profit/loss samples (2-tailed paired t-test, p-value = 0.47). Of course, the yield from random outcomes was based on just one possible sample of random outcomes; re-run the random number generator and we'll get a difference answer. The full population of answers will be normally distributed about an average that can be calculated from the actual expectations. This turns out to be -2.36%, meaning our random sample did a little bit better than the expected average.
Two things are striking about the comparison between the actual and random time series: 1) The trend lines are almost the same; and 2) there is more short term variability in real Pyckio time series than in the randomly generated one. One explanation for the latter might be found in the short term variance between different betting markets. A priori one would expect differences between different sports and different leagues. Indeed such short term difference were observed in the first month after Pyckio's launch, with some football leagues showing strong positive yields and others showing large negative ones. If a disproportionate number of tipsters were concentrating on certain markets compared to others and at different times, this would likely increase the variability seen in the evolution of the bankroll. Another explanation might lie in the fact that the random sample assumes the same profit margin for every bet, whereas this will not be the case for Pinnacle Sports' actual markets.
Finally, one might reasonably argue that the greater variability compared to the random case is evidence of market inefficiency (mistakes that some tipsters were exploiting whilst other were falling victim to), at least over the short time scale. Whether that was indeed the case, would need further investigation. Sadly, however, whatever that investigation might reveal, it would appear that any short term inefficiency in sports betting markets does not last very long. Economists who support the efficient market hypothesis frequently argue that most short term inefficiency soon disappears once it has been discovered, making its long term prediction impossible. Indeed, why would anyone reasonably expect anything else? [There are some reasons, but now is not the time.] Most people are rational most of the time; if they see a way of making money, they exploit it until it disappears. There is a well known story popular with those who support efficient market theory: if you see a $100 bill lying on the ground, it can't be real because someone else will have already picked it up.
So we've seen that tips advised through Pyckio's 6,000+ tipsters have pretty much followed a trend entirely predictable by chance, that is to say they've lost roughly equivalent to that predicted by Pinnacle Sports' profit margin. Let's now take a look at how individual tipsters have performed.
2,138, or 35.4%, of the 6,044 tipsters made some sort of profit (compared to 2,513 or 41.6% in the random case), whilst 3,892, or 64.4%, made losses. 14 of them exactly broke even. On the face of it, more than a third of tipsters making money might look impressive. But we must remember that we can all make a profit simple by luck. The key question is whether the distribution of profits that the tipsters have experienced differs significantly from a distribution that could be predicted by chance. If all we have is luck, luck will eventually run out, and money we might have already made may then be handed back as losses, as the evolution of good and bad luck combined regresses to the mean.
Tipsters are usually rated according to profits and yields, but these measures alone neither take into account the longevity of records nor the betting odds that were used to achieve them. A 1,000-tip history showing a 10% yield from betting at odds of 1.75 is arguably much better than a 200-tip history showing a yield of 50% from betting at odds of 10.00, even though the absolute profits are the same. Instead, it is more instructive to calculate the probability that each record could have arisen by chance by means of the student's t-test. This offers a useful standardisation technique to compare tipsters with different lengths of history and different betting styles (risk preferences). The one sample t-test essentially compares the actual history to that predictable by the odds and their expectations (including the influence of Pinnacle's differentially applied profit margin). Full details of the mathematics behind the T-test can be found in my last book on the truth about sports tipsters.
The chart below plots the distribution of t-test value for the 2,690 tipsters who had histories over 30 bets. The t-test becomes rather unreliable for small sample sizes. Removing the 3,354 tipsters with smaller histories (accounting for 27,404 tips or 2.55% of the whole sample) slightly improves the aggregated performance to -2.27%. Understandably, many of the tipsters with short histories will have given up after early losses. Indeed, the yield for this removed sample is -8.07%. Also shown on the chart is the distribution of t-test scores predicted a priori from random settling of the bets, based on the odds and their calculated expectancies.
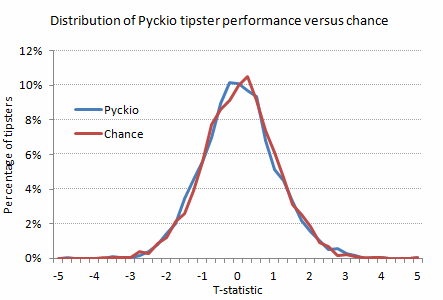
Again, as for the Botprediction analysis in the previous article, spot the difference. Essentially, what tipsters operating through Pyckio are replicating, on average, is exactly that which would happen by chance. Indeed, based on this dataset there is barely even the slightest hint that tipsters in the profitable extreme of the distribution are doing anything better than chance. 69.6% of tipsters fall within plus or minus one standard deviation in t-test scores (1.035), and 95.2% within two standard deviations. For normal distributions these figures are 68.3% and 95.5% respectively. The standard deviation in the random distribution is 1.027, almost exactly the same as for the Pyckio sample.
The 1-in-100 probability that a record might happen by chance rather than skill that I traditionally apply to analysing a tipster shows that just 45 tipsters managed to achieve that performance level. Chance predicts a number of 38. The difference is not statistically significant (chi-square test p-value = 0.25). The best performance from a tipster with a longer record (over 100 tips) was a t-score of 4.06 (based 701 tips and average odds of 1.99), equivalent to a 1 in 37,000 probability that this could have happened just by luck. But the random number generator delivered a 143-tip history (average odds 2.15) that had a 1 in 172,000 probability; food for thought indeed! Clearly, with enough people playing the sports betting game, pretty much anything is possible, just by chance.
What about the really long records, those of tipsters who've stood the test of time? How does their performance compare to random outcomes? 249 tipsters had records of 1,000 tips or more, the largest having 13,645 whilst the average was 2,047. 65, or 26.1% of them, were profitable, a marginally smaller proportion than for the whole sample. The best yield was 6.1% (from average odds 2.11). However, a much greater number of these long-record tipsters managed to "beat" the Pinnacle Sports market (as defined by the t-statistic value being greater than 0), 154, or 61.8%, of them in fact, compared to the 50.3% for the full sample. This is probably to be expected, given that this smaller sample of long-record tipsters offers an example of survivorship bias. Longer records are there simple by virtue of the fact they have survived by doing better for longer; those which didn't survive, never managed to get to 1,000 picks. Of course, "better" in this context doesn't mean actually making a profit, but simply doing better than market expectation, which is defined by Pinnacle's 2.5% profit margin. Consequently, whilst a higher percentage managed to beat that margin, a smaller proportion got above the profit line.
Of course, none of that means these services survived by virtue of anything other than chance. To get a handle on how many might have done so by means of something more, let's compare these figures to the randomly outputted sample. In this case, 36, or 14.4% of them were profitable whilst 140, or 56.2%, outperformed market expectancy. [A priori we should expect this second figure to be 50%, although obviously for smaller samples the larger variance may result in more considerable deviations away from this mean.] The difference between the Pyckio sample and random sample in the number of long-record tipsters actually showing profitability (65 versus 36) was highly significant (chi-square test, p-value = 2x10-7). Furthermore, the difference in the t-test statistics for these 249 Pyckio records versus their random counterparts was also weakly significant (2-tailed paired t-test, p-value = 0.016). And whilst only 7 randomly produced records longer than 1,000 picks showed yields of more than 2.5%, there was double this number, 14, in the actual Pyckio sample (the highest being 6.1%, average odds 2.11, compared to 4.4%, average odds 2.02, in the random sample). Indeed, the chart below showing the distribution of t-test scores for these 249 records hints at the appearance of a profitable fat tail in the Pyckio sample compared to the random sample that presumably must arise by something more than chance.
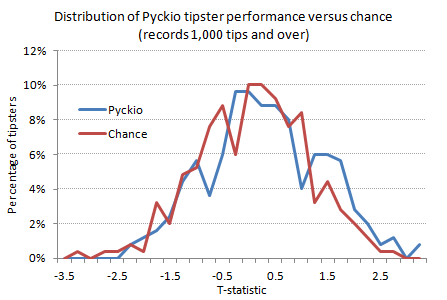
Does this provide any comfort, for those still clinging to the hope that they can predict uncertain futures, that at least a small handful of long-lasting tipsters could be achieving something more than luck? Possibly, although if we reduce the threshold for the number of tips required for a long record, these statistical significances disappear. More troublesome is the fact that these statistical significances may more plausibly have arisen because of the very survivorship bias I described above. Whilst tipsters who initially do quite well (either beating the Pinnacle expectancy or better still making a profit) are more likely to survive through to 1,000 tips or more, the same cannot be said of the random sample. Unlike human beings, my random records were not capable of making decisions as to when to stop and when to carry on. They just did as they were told, which was just to pair match the corresponding Pyckio record with the same number of tips. Consequently, it is probably inappropriate to perform any statistical testing between these two small samples at all, given the inherent bias. More generally, the same can probably be said of any population of tipster records, including the whole Pyckio record of 1,073,029 picks, which will always be dominated by "survivors".
I carried out one little extra investigation into the comparative performance of the big sports compared to the smaller niche ones. In my book I reported that tips from smaller niche markets performed considerable better than those from the big sports, including soccer, tennis and the US sports. Here I have not had the time to go through the dataset to exactly match the categorisation I chose for that earlier analysis of my own sample of verified tips. In particular, included within the big sports is European basketball and ice hockey, which for the analysis for my book I had regarded as niche markets. Nevertheless, the minority sports for the Pyckio sample probably can be considered as such: Australian rules football, darts esports, handball, mixed martial arts, rugby, snooker, table tennis and volleyball.
Sadly it appears no such improved performance existed for these minority sports. The yield from their 55,528 tips (or 5.17% of the total sample) was -2.11%, compared to -2.18% for the remainder. At Pinnacle Sports, at least, it would appear that even the smaller sports are liquid and efficient enough to make it very difficult for almost everyone to do anything much better than chance.
Time to draw conclusions. If ever there was definitive evidence that almost all sports tipsters do almost nothing more than replicate chance, here it is. Of course, to re-iterate, none of this proves beyond doubt that no skill whatsoever is operating. This statistical analysis has nothing to say about skill, merely whether a performance looks something like that which could be predicted by chance. It is conceivable that amongst the 6,000+ tipsters there may be a small few who are genuinely doing what they do with more than just lady luck looking after them. Indeed the analysis of long-term records containing a 1,000 or more tips shows that, survivorship bias aside, some of them at least might possibly be doing something better than that predicted by chance alone. A bigger and better analysis of more tipsters that can properly take into account the described survivorship bias might reveal a more statistically significant profitable fat tail containing skilful tipsters. And Pyckio being the largest (and most transparent) tipster social network online at present is in the best position to find them. Nevertheless, we are clearly not talking about many as a proportion of the total population of people playing this game.
This analysis, then, helps answer a question that has troubled me for many years - how many people win at sports betting? It's frequently quoted that about 95% (sometimes it's a bit lower, sometimes a bit higher) of sports bettors fail to make a profit. But as this analysis has shown, this statistic doesn't help us very much. It's like asking how long is a piece of string; well, it depends, and in the context of sports betting, mostly on how lucky we have been and how long we are betting for. We can see that lots of people win in sports betting, and sometimes over quite long periods. More importantly, however, will they consistently keep winning if they keep betting, and can they predict that, or has what has happened to date simply been a matter of chance? The data from Pyckio - and it's undeniably a very large dataset - fairly emphatically reveal that if any skilled forecasters in the world of sports betting really exist, they probably aren't numbered in one-in-tens or one-in-hundreds but perhaps one-in-thousands or even one-in-ten-thousands. Everybody else is just tossing coins, whether they like it or not. Why this should be so, why sports betting markets, well, Pinnacle Sports' market at any rate, is so efficient, with virtually no opportunity to consistently and predictably beat the market through something other than luck for almost everyone playing in it, is perhaps the next interesting question, but that is for another time.
|





