Luck Versus Skill in Sports Betting: Analysing a Betting Record
Posted 30th May 2013
Earlier this week I received some SPAM from William Murphy Sports Investment and Advice Forum telling me that it had hit 66% winners since the current soccer season had started from over 200 picks. So what? Yes, it was free, but telling me that you have a 66% strike rate doesn't tell me very much, does it? Presumably anyone could achieve a 66% strike rate backing Barcelona or Manchester United all season, but it probably wouldn't make much of a profit.
To be fair, all picks were documented with (American) prices. A rough inspection of a few of the forum pages revealed that the vast majority of prices tipped were odds-on, with an average in the region of about -150, that's about 1.66 to Europeans. This actually translates into a betting yield, or profit over turnover, of about +10%. Not hopeless but not spectacular either. The really important question to ask, however, is whether I could do just as well picking plays at random and simply hope to get lucky, and if so, how often I could expect such a return. Knowing whether we have any genuine forecasting talent or whether we are just plain lucky is really the key to long term success in sports betting.
In both my books Fixed Odds Sports Betting and The Truth About Sports Tipsters I have discussed at length the techniques we can use to analyse a betting record and test how likely it will come about by chance alone. These include the Chi square test, the t-test and the Monte Carlo simulation. Broadly speaking all tests involve the comparison of the betting record with a baseline average, in other words what one would expect to happen over the long term should there be no skill involved whatsoever.
Imagine tossing a coin. We don't know if it is a regular coin or if it is weight-biased in some way. Over the long term we would expect to see 50% heads and 50% tails from an unbiased coin. Suppose we toss it 20 times and 8 of those tosses are heads. What can we say about the coin? Well, if we assume that the coin is unbiased (our null hypotheses) then we should expect there to be a 50% chance of landing a heads on any particular throw. To calculate the chance of landing 8 heads out of 20 we then just need to calculate the individual chances of landing exactly 8 out of 20 heads and multiple it by the number of ways 8 heads can be landed in 20 throws. In fact the answer is a shade over 12%. We can perform exactly the same calculation for all possible numbers of heads fewer than 8, i.e. 0 through 7. Adding these altogether gives us the probability that we will throw 8 heads or fewer in 20 throws of an unbiased coin. This comes to approximately 25%. In other words, about 1 in every 4 sets of 20 coin tosses, we should expect to see 8 heads or fewer, provided the coin is unbiased.
What if we tossed the coin 100 times and landed no more than 40 heads, in other words the same proportion of maximum heads to total coin tosses as before? This time, the probability of landing 40 heads or fewer is just 3%. Why so much smaller? Simply because we have thrown the coin more times, and the more times we throw it the more likely that the number of heads landed will approach the long term expectancy of 50% for an unbiased coin. This is simply a consequence of the law of large numbers.
What if we tossed the coin 1,000 times and saw no more than 400 heads? This time the probability of this occurring by chance for an unbiased coin would be just 1 in approximately 7 billion. At this point we might reasonably conclude that the probability of this happening purely as a result of luck is so remote that the coin must be biased in some way towards landing tails.
Essentially, when comparing a betting record to a nominated baseline average we are performing exactly the same analysis of luck versus something else. For coin tossing, the reasonable assumption would be that the something else is weight bias. In sports betting it would be reasonable to conclude that the something else, for an honest record at least, is skill at predicting outcomes. When performing such a test, there are basically just two parameters we need to define to arrive at a conclusion. 1) What are we measuring the betting record against? In other words, what is the baseline long term average, assuming the null hypothesis to be true? 2) At what level of probability do we decide that it probably isn't luck that is explaining the observation? Both parameters involve an element of subjective assessment.
The baseline average is simply what we should expect to occur over the very long term, or more precisely over an infinite amount of time. For unbiased coin tossing this is obvious. It's simply a 50-50 proposition so over an infinite number of tosses the number of heads and number of tails would both tend towards 50%. For sports betting, it's a little less straightforward since there is the added complication of the bookmaker's advantage, which varies from bookmaker to bookmaker, from sport to sport and from betting market to betting market. If we simply bet randomly on Premiership match bets taking average market prices we would expect to lose about 8% on our total investment over the long term. By contrast if we just bet with Pinnacle Sports, we might only expect to lose 2%. If on the other hand, we bet on golf outright tournament markets, our expected losses would be anything from 20 to 60%. Of course, it would be true to say that most educated punters know how to use an odds comparison and how to find the best market prices. For the majority of heavily traded match bet markets in the popular sports, best prices represent a close approximation to 100% market efficiency, in other words 100% value or break even. Using such an assumption, then, our baseline average essentially becomes break even or zero. If a punter (or tipster) is doing little or no better, then the implication is that he is simply just guessing (or he is not very good at finding best prices).
So what about luck and when can we begin to rule it out? In the coin tossing experiment it would appear pretty self-evident that landing 8 heads out of 20 would not be evidence of a biased coin, given that there is a 1 in 4 chance that it should happen for an unbiased coin. Similarly, landing 400 heads from 1,000 tosses would offer pretty definitive evidence for the coin being biased, with a 1 in 7 billion expectation that it would happen for an unbiased coin. What about the 40 heads from 100 tosses? A 3% probability is small, but not tiny. With a 1 in 33 probability of it happening by chance, could we reasonably conclude that the coin is probably weighted? In fact, statisticians performing such tests defined what are termed confidence limits. Traditionally these have been the 95% and 99% confidence limits. Turning these around, they are basically equivalent to 5% and 1% probabilities respectively of something happening purely by chance alone. At 3%, 40 heads in 100 tosses comes between these two confidence limits. Some statisticians might argue the case for the coin being biased, others might still suggest chance is probably still at work. Personally speaking, when it comes to analysing sports betting records, I prefer the 99% confidence limit. Indeed, I think there is a strong case for it being even higher, for example 99.9% or 99.99%. But that is for another time.
So let's return to our friend William Murphy. With a 10% yield from 200 picks at average odds of about 1.66, what is the probability that this return on investment would simply happen by chance? Whilst the testing is a little more complex than for the straight binomial analysis that can be used for 50-50 coin tossing experiments, the statistical process of hypothesis testing is essentially the same. Throughout my analyses of tipping records in The Truth About Sports Tipsters I made use of the t-test. I also presented a neat little approximation that could allow readers to quickly and easily test statistical significance of a record, simply by knowing only the yield, number of bets and average betting odds. This approximation of statistical significance is fairly robust for bet samples larger than 100 and where the stake sizes don't very too much across the betting odds. Ideally it is suited for level stakes betting histories. For readers here, I have created a little downloadable file to allow the testing of any simple betting record, whether their own or someone else's. Plugging William Murphy's figures into this worksheet calculator (200 bets, 0.1 decimal yield (or 10%), 1.66 average odds) returns a decimal probability or p-value of 0.037, equivalent to a chance of 3.7% or 1 in 27. At my chosen confidence limit, I do not yet consider this betting history to be evidence of any real forecasting ability. With a yield of 10% at these betting prices and after just 200 selections I cannot not rule out the possibility that it hasn't all happened simply by chance. After all, provided the tipster was betting market efficient 100% value prices, we would expect this to be replicated once on every 27 times.
What if he did it again over the next 200 bets? Well, then things become more interesting. This time, the p-value drops to 0.006 with a 1-in-178 probability of such a return occurring by chance. To achieve that level of statistical significance from 200 bets William Murphy would needed to have hit a 14% yield. Alternatively, a yield of 10% from 200 picks could achieve this greater statistical significance if the betting prices had averaged 1.38 rather than 1.66.
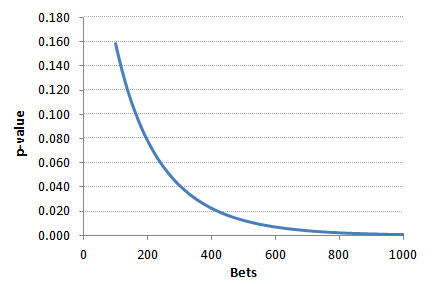
Sheet 2 of the spreadsheet charts the relationship of the number of bets (up to 1,000) with statistical significance (the p-value) for specified pairs of yields and betting odds. Feel free to try it out. The relationship for a yield of 10% at even-money betting prices is shown below. In particular notice how records with longer betting odds are much less statistically significant than those with shorter betting odds for the same yield and number of bets. This is simply a consequence of the greater inherent randomness involved when betting lower probability propositions. If my yield is 10%, I will need about 540 even-money betting propositions before I can conclude that something other than chance might be accounting for my performance. I would need a yield of about 34% betting at prices of 9/1 (10.0 in European format) if I was to demonstrate a similar level of statistical confidence in my forecasting ability from the same number of bets.
Needless to say, when I presented my forthright observations about William Murphy's soccer picks record, they were not met with understanding or appreciation. The reality is, however, that too many sports punters and tipsters fail to give enough thought to what their betting record is telling them, and in particular whether they have properly assessed whether it has anything more to do than just chance alone. Lady luck will frequently deliver profits in the short term, but if the player wrongly believes that something else is going on the long term will surely catch them out, and only the bookmakers will be smiling. Testing the presence of skill against a background of luck is simple enough provided you know what you are doing. To that end, I am at everyone's disposal to provide assistance in performing such statistical testing of a betting record.
Before closing this article, it's worth spending a bit of time using this methodology to determine when a record appears to be just too good to be true. I've seen enough of them in my time to know that if there is one other certainty in sports betting in addition to a bookmaker having maths on his side, it's that there will always be someone willing to pull a fast one. The essence of sport betting is taking risk positions to make money. At the heart of it is a desire to become richer, which unless managed and controlled will quickly turn into greed. Greed breeds greed, and for every punter desperate to succeed will be another happy to sell him a lie.
In researching this article I came across Fixed-Bets.com. The name rather says it all. Fixing matches is illegal for obvious reasons. People engaged in it damage the sport and the betting facilitated by the sport. The only winners are the ones committing the fraud. Of course, whilst they do exist, the numbers who are genuinely engaged in fixing matches is thankfully relatively small, far smaller than the number of websites selling fixed matches would have you believe. Fixed-Bets.com claims to sell "insiders". That may not mean "fixed", but presumably at the very least it means selling picks that they know something about which everyone else does not. Of course, if such insider information was genuinely for real, the betting market would soon re-establish itself at prices that reflected the insider information. As soon as insider information gets outside, by definition it is no longer insider information. A random check of a few of Fixed-Bets.com's results reveals there is no significant price shortening of betting prices which have been advised.
Through to the 29th May 2013, Fixed-Bets.com has a record of 166 tips dating back to the 31st October 2012. With the exception of a 29/1 double-result pick (which won, and which I have removed for the purposes of the following analysis) all the selections were priced between 1.55 and 4.5, with an average betting price of 2.28. Of these 165 selections, 146 were winners. That's a strike rate of 88.5%!!! Not even Barcelona and Bayern Munich have win rates as high as that this season and their average odds will be something like 1.4 home and away. The yield for this betting history is a stratospheric 103%, not the return on investment, the yield. (That rises to 120% if I leave the 29/1 shot in the record.) And the growth trend when plotted on a chart makes for an almost perfect straight line. Plugging these numbers into the P-value calculator returns a probability of approximately 2 in a hundred thousand trillion, trillion, trillion (that's 2 followed by 41 zeros) that this history would arise by chance alone. That is marginally less likely than the probability that I find all the atoms in my body spontaneously relocated to the surface of the moon in their current arragement, as dictated by quantum mechanics, at some point during the time it has taken me to write this article.
Of course, Fixed-Bets.com would presumably wish to argue that all this proves is that they know their insider information. I would conversely argue that all they know how to do is cheat. As argued, if they weren't cheating and this information was genuine, then such insider information, sold at just €50 per "fixed match", would quickly cause a huge price shortening by the bookmakers, something that has not been witnessed. Furthermore, if you had your hands on information that effectively offered a fair price of 1.13 (or 1/0.88.5) for 2.28 with the bookmakers, why would you need to sell it at all? Keep it to yourself, and instead just bet the maximum stake limits at Pinnacle Sports and other bookmakers happy to tolerate winning punters. With £10,000 stakes you would already be closing in on £2,000,000 since only last November. And many of the matches would allow much bigger stakes than that.
The truth, of course, is almost certainly that the picks are fake. The likelihood that so many matches across such a large spread of European football divisons would be fixed without the football associations, never mind the bookmakers taking the bets, knowing that something was wrong, is surely remote indeed. Knowing how to test the significance of a record can help you tell apart the fake from the genuine, just as it can help find evidence of skill against a background noise of luck.
|





