All Monkeys Are Throwing Darts. But Some Monkeys Are Better Than Others
In 2015 I wrote the book Squares and Sharps, Suckers and Sharps: The Science, Psychology and Philosophy of Gambling which presented the evidence that sports betting, to a very significant extent, is little more than a game of chance, just monkeys throwing darts if you will (which indeed became the title of one of the chapters). I re-emphasised my view in my latest work, Monte Carlo or Bust: Simple Simulations for Aspiring Sports Bettors.
As a consequence of my stance, I was infamously labelled by a former Pinnacle podcast host the 'grim reaper of betting'. In defence, I always maintained that I was prefixing my position with the word "almost". 'Almost all chance' is not the same thing as 'all chance'. Indeed, I am well aware that bettors and tipsters do exist who demonstrate skill beyond luck, it's just that I insisted there were very few of them and very hard to spot.
Well, I was wrong!
Before readers get too carried away with the idea that everything I've previously said about skill versus luck in sports betting was nonsense, I should qualify what I mean by 'wrong'. It is still true to say that sports betting is a very hard nut to crack. It is still true to say that very few people aspiring to crack it will be successful in the long term. It is still true to say that almost everything that happens in terms of profits and losses for people who bet is just luck. What is not true is that almost everyone who bets are unskilled. Betting skill, or what I will henceforth call betting IQ, is in significant abundance. I had previously just been looking for it in the wrong place. This article will reveal how I found it, and flesh out why I have chosen to put my updated beliefs about this topic on the record.
Why Betting Looked Mostly Random
In 2015 I took a good look at the betting performances of over 6,000 bettors active on the tipster supermarket platform Pyckio.com. Responsible for over one million bets during my analysis period of June 2014 to February 2015, not only did their aggregated performance trend closely to the expected loss predicted by Pinnacle's margin, but their risk-adjusted individual performances (as measured by the t-score which takes into account both the length of the betting record and the odds of the picks) were as close to being normally distributed as would be predicted by chance alone. Most damning of all was a complete lack of persistence in bettor performance over time, with almost complete mean regression. It was effectively impossible to use a bettor's performance to predict how they would perform going forward. It was as if they were all (or almost all) just chucking darts as monkeys would, or just tossing coins.
Analysing a more recent set of Pyckio data (over 600,000 picks from over 1,500 tipsters), I confirmed these findings. Bettors' t-score were normally distributed and there was complete mean regression between a bettor's first and second half performance, as shown in the scatter plot below for the 887 bettors with a minimum of 200 picks (100 for each half).
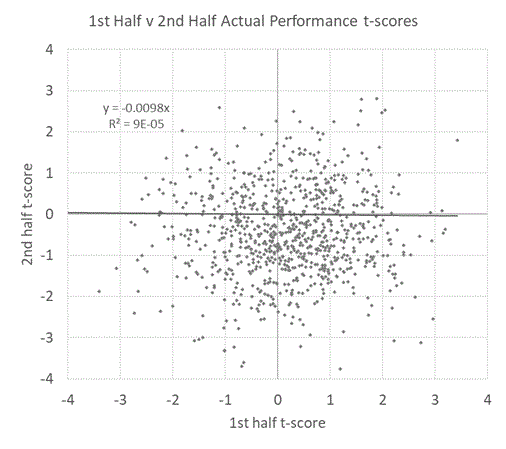
Effectively none of the variance in the first half (risk-adjusted) performances of these 887 bettors explained the variance of the performances in their second halves. Again, it's just as you would expect if all they were doing was rolling dice, and if all they are doing is rolling dice, surely there's no skill involved in that, right?
Looking in the Wrong Place
Betting outcomes, as we know, are hugely subject to chance. I've done a large amount of work, particularly in Monte Carlo or Bust, showing how a bettor's outcomes over a range of possible histories will distribute normally. The consequence of this chance (what is more formally called aleatory uncertainty) means that the outcome probabilities between winning and losing bettors can sometimes be surprisingly small. For a betting history of 100 bets, for example, a bettor losing to a 2.5% margin can expect be showing a loss 60% of the time. It's still as much as 40% for a winner expecting to make a profit of +2.5% as a percentage. Even over 1,000 bets, it's still 20%.
Perhaps, then, looking at betting outcomes, even risk-adjusted t-scores, is not the right place to look for any evidence of skill. If it is there, it can't be seen because there is simply too much noise in the business of betting results. Is there another place we can look?
Expected Profits and Closing Line Value
In 2019 I wrote a piece for the Pinnacle Betting Resources looking at how closing line value (or CLV for short) might help test for evidence of a bettor's skill. In an information market, where the price of something is determined by how much people know about it, betting on superior information that you may hold over the rest of the market should, in theory, reduce the price. In point spread markets familiar with US sports bettors, this is equivalent to moving the line. For fixed odds markets more typical in Europe, it will be the odds that will shorten.
Traditionally it has been assumed that the most accurate line or odds exists just as the market closes and the game starts, because that is the point at which most information has come to the market. This does not imply the odds are perfectly true (or efficient), just better, in theory, than what came before. Hence, by comparing the odds (or line) that you bet to the closing odds can provide a useful measure of your value in your bet (hence the phrase closing line value). If you are able to consistently bet odds that shorten by the close, this can perhaps be used as a proxy measure of your betting skill.
In my 2019 article I show how much faster the CLV could be used to find evidence of skill compared to betting outcomes alone. What might take thousands of bets to determine if a profit is statistically significant by looking and wins and losses might take only 50 to 100 using the closing line. Why? Simply because the variance (or noise) in the closing line is so much smaller than the variance in results. We also know that bookmakers who limit customers sometime manage to restrict after only a handful of bets. They couldn't possibly do this using results alone; furthermore, if they did, it would not explain why they limit customers showing losses too. The most common metric they will use to identify a sharp bettor will be their closing line value. A couple of former traders have confirmed this with me.
A Lesson in Confirmation Bias and Bayesian Belief Updating
All of this begs the question: If I knew about the power of CLV to detect skill in 2019, why didn't I use it to search for skill in the Pyckio data set? Well, firstly I didn't have the data; secondly, and more importantly, it just didn't occur to me. I was too consumed by my own conformation bias about the randomness of betting for the idea to come to my attention.
To shake me from this oversight, I must thank Betting Twitter aficionado @aluckyaday who has a never-ending capacity to challenge accepted wisdom. His belief here was that if betting IQ was like other skill sets, it should be normally distributed (the bell-curve). If that was true, then this would account for the normal distribution of outcome t-scores. More skilled bettors would have better results; less skilled bettors, worse results, but all would be normally distributed because the underlying skillset is normally distributed.
“Hang on,” I argued, “this might be true, but why do we see complete mean regression over time?” His counter claim was that looking at results was not the right way to test for skill. Why? Because there's too much noise (the aleatory uncertainty). Whatever skill may be there, it will be hidden and take thousands or even tens of thousands of bets to appear. In the scatter plot of 887 bettors above, the average bet number is just 610.
"Then find some in the CLV," I said.
Using CLV to Test for Skill in a Bettor Population
In 2015, when I first tested the Pyckio dataset, I only had results to look at. However, in January 2021, betting expert @BettingIsCool began collecting the CLV of all Pyckio's tipsters. I used this dataset earlier in the article to confirm that betting performances as measured by profits and losses were completely regressing to the mean. I could now also use it to test two new questions: are bettors' CLVs normally distributed, and do they show persistence over time?
Regarding the first question, more specifically I wanted to see if the risk adjusted CLV was normally distributed. CLV, just like profits and losses, will be more variable the longer the odds one is betting at. Again, standardising for this influence, as well as the influence of the length of the betting history, can be achieved via the t-score. How did the CLV t-scores of this 1,525-bettor population distribute? Take a look below.
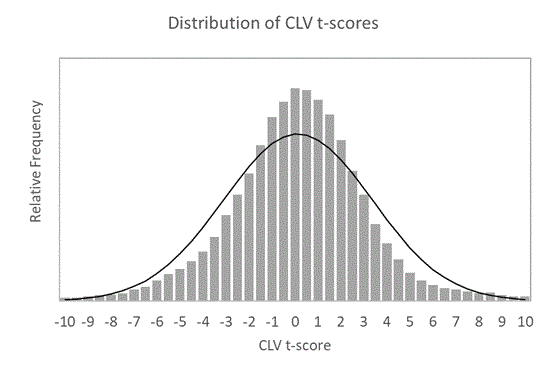
The histogram shows the actual CLV t-score frequencies. Over this, an idealised normal bell curve is superimposed. You can see that whilst there is clearly a symmetrical spread in CLV t-scores, the distribution does deviate somewhat from an ideal normal distribution. There are fewer outliers. Nevertheless, it does clearly demonstrate that the distribution of CLV (and by extension betting IQ, if CLV is a useful proxy measure of that) varies significantly. It is just not the case that the betting population is comprised of a few sharps and a whole load of squares with no skill at all.
We can qualitatively gauge how much betting IQ, as measured by CLV, is present. Even if there was no betting IQ present in this population at all, the CLV t-scores would still randomly distribute, and it is easy enough to determine by how much. I've done this in the next chart below and compared it to the actual CLV t-scores distribution.
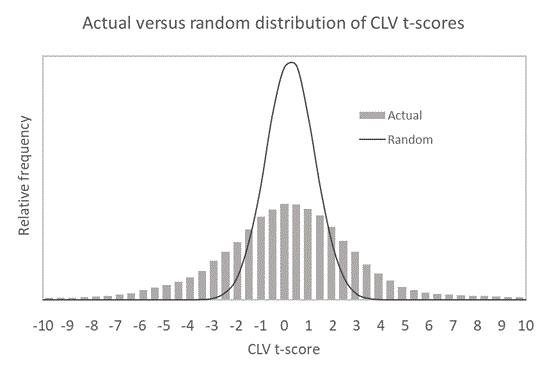
The actual distribution of CLV t-scores is much greater than if there was no betting IQ at play. You can see just from the magnitude of the t-scores themselves that bettors' betting IQ varies from very impressive to truly terrible. Not only are there bettors in this population who are supremely gifted at finding CLV, there are others who are so bad, they are actually performing far worse than if they were just guessing. It's probably those cognitive biases at work here. T-scores anything beyond about plus or minus 3 imply less than a 1-in 1,000 probability that they could happen by chance. The fact that we see many more than 1-in-1,000 in this population implies there's more than just randomness going on in the bettors' CLV. This relates to a point I've made in my previous article on closing line value: if you see it, you usually see it quickly (much quicker than evidence of skill from results) and you can be almost certain it's causal and not random.
That's the good news. Here's the bad. Keep in mind here that a t-score of 0 broadly equates to losing the equivalent of Pinnacle's margin, which in this dataset was around 3%. Most of those bettors in the right-hand side of the distribution were still expected to lose money based on their CLV. In fact, of the 1,525 bettors, only 60 actually had a profitable CLV, and close to three-quarters of those were actually not statistically significant (taken as p-value less than 0.01). They may have statistically significant betting IQ (as judged by CLV), but for the vast majority of the time it's not enough to overcome the bookmaker's margin. This just leaves about 1% of bettors in this population where I could confidently say their CLV would be sufficient enough to secure long term profitability that I would believe is not just down to good fortune.
Is CLV Persistent Over Time?
The real test of whether something is random or causal is whether it persists over time. If it does, it suggests the latter; if not, and we see only regression to the mean, it implies the former. As for the analysis comparing first half and second half outcome t-scores for the 887 Pyckio tipsters with at least 100 picks in each half of their betting history, I repeated the same for the CLV t-scores. Their correlation is shown in the scatter plot below.

The correlation is strong, with the variance in the first half CLV t-scores explaining half of the variance in the second half CLV t-scores. A regression test demonstrates that the probability this correlation is random is effectively zero. This is robust evidence for persistence in a bettor's ability to find CLV. Whilst their results might regress to the mean over hundreds or thousands of bets, their CLV does not. It's not a perfect correlation, but then CLV will not be a perfect proxy measure of betting IQ.
Nevertheless, such a strong correlation provides further evidence for the validity of the closing line value hypothesis that I discussed at length in Monte Carlo or Bust, at least in more efficient (accurate) betting markets that Pinnacle is renowned for. Those continuing to question the hypothesis will again be forced to explain why such a persistence in CLV over time exists. If it's not random, it must be causal, and if the cause is not a measure of betting IQ, then what it is? Furthermore, those doubting that CLV predicts actual profitability should know that the correlation between these two metrics, whilst weak (R2 = 6%), is statistically significant. Despite the huge variance in profit/loss outcomes, those bettors with superior CLV tend to make more profit over the long term.
Some Final Thoughts
In one sense, all monkeys are indeed throwing darts. The noise of results in betting means that nearly everything that happens over the short term is almost all a consequence of good and bad luck. Over durations of hundreds to thousands of bets, bettor profitability regresses to the mean. What money a bettor makes over such a period is effectively useless at helping us predict what they will make over the next similar period. This still largely applies even for the bettors with the highest betting IQ. For the 60 bettors with profitable CLV, the variance in first half profits/losses explains only 8% of variance in second half and numbering just 60 was hence not statistically significant. Mean regression still dominates. If we are to find evidence of persistence and skill in the betting results, we are going to need many thousands, if not tens of thousands of bets to uncover it.
Not all monkeys are equal, however. Whilst there's a lot of randomness in their dart throwing, hidden within is a much narrower variability in skill. We can't see it in profits and losses, but we have found it in the proxy measure of closing line value. The skill involved in finding closing line value persists over time, and over the much longer term will ultimately prove to be a reasonably valuable predictor of profitability. But ‘longer term' really is a long time. The variance in profits and losses for this population of Pyckio bettors was 75 times larger than the variance in CLV. True score theory tells us that variance in outcomes is the sum of the variance in skill plus the variance in luck. This tells us that here, luck is accounting for nearly all the variance in outcomes. No wonder I could never find any evidence of skill in the profits and losses.
Last but not least, whilst we may have found in the distribution of bettors' CLV a usual proxy for the distribution in betting IQ, for nearly all bettors in the efficient betting markets that Pinnacle specialise in, it's not enough to overcome the betting margin. The distribution of sharps and squares may be different to how I had initially visualised it, but betting still remains a hugely difficult competition to succeed in, where the margin a bookmaker imposes along with access to some of the best forecasters in the business means only a tiny minority will be successful in the long run. Yes, it's possible less efficient markets will support a larger proportion of winners, but those markets will also have smaller staking limits, and the bookmakers who facilitate many of these more inefficient markets have reputations for refusing sharp custom anyway. Good luck with your dart throwing.
|





