What is the true expected profit for the Wisdom of the Crowd Betting System?
Since 2015 I have been posting live bet suggestions on my website for my Wisdom of the Crowd betting methodology. Strictly, it should be called the Wisdom of the Pinnacle Crowd, or even Wisdom of the Pinnacle odds compilers and their small cohort of sharp customers, for reasons that will be clear if you read the methodology document. First published in Squares and Sharps, Suckers and Sharps: The Science, Psychology and Philosophy of Gambling, and again more recently in Monte Carlo or Bust: Simple Simulations for Aspiring Sports Bettors, if you haven't yet seen it, I'd urge you to take a look. To my knowledge, it's the only openly and freely published sports betting methodology that has been proven to work. If you don't believe me, try it for a few months with stakes larger than your 7-year-old's pocket money with no other attempt to disguise your activity, and if you don't find yourself restricted by any bookmakers, I'll wager you must be the betting equivalent of the Invisible Man.
In this article, I don't want to go over the methodology again. Neither do I want to question whether the results are just lucky. I think it's pretty clear that after nearly 16,000 live-published bet selections, the methodology works. According to the profit chart published on the website, the actual profit trend almost perfectly matches the expected one. For information on how the expected profit is calculated, again I urge you to read the methodology, either on the website or in one of my books. There is, however, one aspect of the way the expected profit is calculated that I do want to query here: which odds do we use?
Over the last 6 years I've published a fair amount of material at Pinnacle's Betting Resources on the subject of odds efficiency or accuracy. The more efficient or accurate the odds, the more reliable they are as a reflection of the true chances of teams winning. The reason this betting methodology can exist is because Pinnacle's odds are more efficient than other bookmakers; indeed, they offer a good reflection of the true odds, meaning that we can use them to bet prices from other bookmakers when those are longer than Pinnacle's (having removed the margin from Pinnacle's odds - here I am using my 'margin proportional to odds' method). But which odds do we use?
Theory suggests the most efficient odds to use are the closing odds, or the ones available just before kick-off. This, of course, presents a problem. We can't know what those closing odds are going to be if we want to take advantage of inaccurate betting prices at other bookmakers before kick-off. The best we can do is use Pinnacle's odds at the time we check the market. This, of course, is exactly what I have been doing when live-publishing any matches selected by this methodology on my website. The question is: when retrospectively calculating the expected profit for a bet, should I use Pinnacle's odds at the time I find the value, or recalculate based on the closing odds?
Because of odds movement, doing the latter will inevitably mean that some bets that were demonstrated to hold value at the time they were found would thereafter lose it, if judging that value retrospectively by the closing odds. Indeed, from my own data analysis, as much as a third of the bets shown to have some positive expected value will lose all of it by closing, if judging the true value by the closing odds. Of course, other odds move in the other direction, increasing their value as judged by the closing odds; as always, we are interested not in true value on a bet-by-bet basis, but rather the average value over a large sample of bets. We should, however, be interested in whether that average is significantly different between the odds used at the time the value is first found and the value as judged by the closing odds. If there is a significant difference, it might bring into question whether some of the observed actual profit is a result of luck. We need to analyse some data.
Using a data sample of Pinnacle's closing odds going back to the 2012/13 season (3 additional seasons to the live record published on the website), the chart below shows a time series of actual profit (from level stakes) accumulated from 26,960 1X2 bet selections (from main league European football) that achieved the system criteria (minimum expected value of 2%). The blue line shows the actual profit trend, which has a final yield of 4.90% (average odds 3.83). This can be compared to the expected profit trends calculated first using the value at the time the bets are found (red line), and second the value calculated retrospectively using the closing odds (green line).
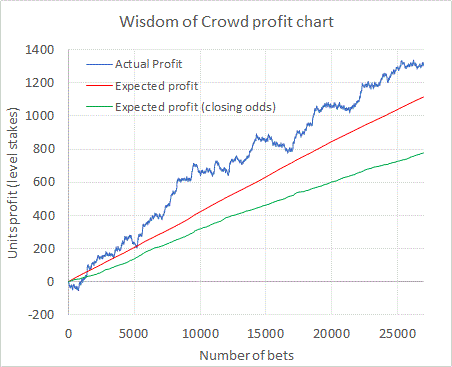
There's a noticeable difference between the two expected profit trends. The red line has a final yield of 4.13% whilst the green one has one of 2.88%. We can see that the actual profit line outperforms both expected profit lines, although for the latter two-thirds, covering the period since live-publishing, the blue and red lines have roughly tracked in parallel (as can be seen in the record on the live-publishing page). For the whole record back to 2012/13, the actual performance has been luckier than expected, but much more so relative to expectation as calculated using the closing odds. None of this, however, tells us which expected profit line is the more reliable one, and how luck the record is.
Many would argue that we should really be comparing the blue line to the green line. The closing odds are, after all, theoretically the most efficient (accurate odds). This would mean that getting on for half the observed profit is just the result of luck. How lucky? Well, we can perform a statistical t-test comparing the two lines (or more specifically the averages). Doing so gives a p-value of 0.05, on the cusp of weak statistical significance. To put it another way, the difference between blue and green is such that only 1 out of 20 times we'd expect the blue line to be so lucky (or unlucky had it been trending lower than the green line - I've performed a 2-tailed test). Yes, statistical significance is very weak, but I do begin to wonder whether the green line really is the reliable measure of true expected profit theory would hold it to be.
Performing the same t-test between the blue and red lines gives a p-value of 0.47, i.e., no statistically significant difference whatsoever. Does this mean the red line expected value is more reliable? If so, what does this say about the theory that closing odds are more accurate?
If we are to abandon the theory of closing odds = more efficient odds, at least for this sample of matches, then we need a credible hypothesis for why we might do so. Fortunately, I think there is one: arbitrage. Pinnacle are proud of their claim never to restrict or close the accounts of winning bettors. This also includes arbitrage bettors for the simple reason that on average Pinnacle are, from their perspective, the right side of the arbitrage. Arbitrage bettors who use Pinnacle for one (or more) match outcome, will, for these bets, be showing losses over the long term. Their profit, which more than compensates for these losses, comes from the other bookmakers, which of course is why those bookmakers hate and ban arbitrage bettors if they can uncover them.
Because of the high stakes needed to make meaningful profit from these arbitrage bets, Pinnacle may arguably be seeing a large amount of action on the other match outcomes. For example, if the other bookmakers are inefficient (too long) on outcome A, a lot of action at Pinnacle for option B (and/or C) may eventually force, or indeed even encourage, them to move away from efficient prices that they like to publish, particularly if that means a greater overall profit from the market. By this reasoning then, arbitrage markets, then, are more likely to be less efficient markets from Pinnacle's perspective. If the odds for outcomes B and/or C are shorter than they should be by closing, then those for outcome A will be longer than they should be. This would then be reflected in the average closing odds in such a sample being longer than the pre-closing odds, and by this reasoning also less efficient than the pre-closing odds for this sample. Is that something that is observed? For the 26,960 bets, the average pre-closing and closing odds are 3.63 and 3.76 respectively. Perhaps more interestingly, that's a bigger difference than for the average odds for the whole data population (74,100 matches and 222,300 odds), 3.58 and 3.62.
But are the matches where we find the methodological value actually matches available for arbitrage opportunities? Again, we can check the data to find out? For the whole data population of 74,100 matches, 19.0% of them held an arbitrage opportunity with Pinnacle odds for one of the three match outcomes (home, draw or away at the time I was searching for the Wisdom of Crowd value). By contrast, for the 22,960 matches where there was at least 2% value from the system methodology in one of the match outcomes, 48.8% of them would have been available for arbitrage. This rises to 60.3% and 73.0% for value thresholds of 3% and 5% respectively. Evidently, a lot of the matches that the Wisdom of Crowd methodology uncovers may potentially be seeing a lot of arbitrage turnover.
Without access to Pinnacle's actual betting turnover figures, we obviously cannot prove that arbitrage is the explanation for why Pinnacle's odds for my system bets with other bookmakers lenghten, the expected value as calculated by the closing odds is lower, and hence by extension less accurate (because the odds are less efficient). However, I think the case I presented is compelling. If nothing else, it may help to account for why after 10 years, and 7 of live-publishing, the actual profit continues to trend away from the closing odds expected profit line. If so, we can therefore conclude that the actual performance, with the exception of the first 3 years in the profit chart, has not been so much lucky, but simply showing more or less what we could expect to see. More generally, closing odds are indeed more accurate than anything before them, at least on average. However, for arbitrage-heavy samples, this make not necessarily be the case, as this analysis may have revealed.
|






